统计机器学习

机器学习

人工智能

发布日期: 2022-12-09

更新日期: 2024-04-15

文章字数: 1.4k

阅读时长: 5 分

阅读次数:

学习的类型

1. 监督学习（supervised learning）

监督学习可以被视为一种学生学习的过程，即向导师提问并回答。在机器学习情境中，学生对应于计算机，导师对应于计算机的用户;计算机从问与答的成对样本中学习一种从问题到其答案的映射。

监督学习的目标在于获得 泛化能力(generalization ability) ：一种能够为从未被学习过的问题猜出恰当答案的能力。

监督学习的典型任务：

回归(regression) ，当答案是一个实数值(如:温度)
分类(classification) ，如果答案是一个分类值(如:“是"或“否”)
排序(ranking) ，如果答案是一个数列值(如:“好”“中”或“劣”)

2. 非监督学习（unsupervised learning）

非监督学习被认为是，导师不存在并且学生自学。在机器学习情境中，计算机通过互联网自动地收集数据并且尝试在没有用户任何指导下抽取有用的知识。因此，非监督学习比监督学习更加自动化，尽管其目标不一定指定清楚。

非监督学习的典型任务：

聚类(data clustering)
异常点检测(outlier detection)
变化检测(change detection)

3. 强化学习（reinforcement learning）

强化学习与监督学习类似，也是以使计算机获得对没有学习过的问题做出正确解答的泛化能力为目标，但是在学习过程中，不设置导师提示对错、告知最终答案的环节。相反，导师评价(evaluate)学生的行为并给予其反馈。强化学习的目标是基于来自导师的反馈，使得学生提高其行为，从而最大化导师的评价。

4. 高级主题

半监督学习(semi-supervised learning)
集成学习(ensemble learning)
矩阵学习(matrix learning)、张量学习(tensor learning)
在线学习(online learning)
迁移学习(transfer learning)
降维(dimensionality reduction)

5. 其他热点

关联规则挖掘
概率图模型
深度学习
图、视频、文本、音频、网络的分析
分布式计算

两种学习模型：判别式模型和生成式模型

监督学习：分类、回归、标记

概率方式
- 判别式模型：直接对 $p(y|\boldsymbol{x})$ $p (y ∣ x)$ 建模或者学习 $y=f(\boldsymbol{x})$ $y = f (x)$
  - 逻辑回归(Logistic Regression)
  - 条件随机场(Conditional Random Field，CRF)
- 生成式模型：学习联合概率分布 $p(\boldsymbol{x},y)$ $p (x, y)$
  - 朴素贝叶斯(Naive Bayesian Algorithm)
非概率方式
- 线性回归(Linear Regression)/岭回归/LASSO
- 样条回归(Spline Regression)
- 支持向量机(Support Vector Machine，SVM) ：基于间隔
- K近邻(K-Nearest Neighbor，KNN) ：基于距离
- 决策树(Decision Tree) ：基于树的节点

非监督学习：降维、聚类、特征学习、概率密度估计（生成数据）

概率方式
- 生成模型：直接对 $p(\boldsymbol{x})$ $p (x)$ 建模
  - 高斯混合模型(Gaussian Mixture Model，GMM)
  - 隐马尔可夫模型(Hidden Markov Model，HMM)
  - 因子分析(Factor Analysis，FA)
  - 概率主成分分析(Probabilistic Principal Component Analysis，P-PCA)
  - 概率潜在语义分析(Probabilistic Latent Semantic Analysis，P-LSA)
  - 潜在狄利克雷分布 (Latent Dirichlet Allocation，LDA)
- 深度生成模型：利用神经网络来建模 $p(\boldsymbol{x}|\boldsymbol{z};\theta)$ $p (x ∣ z; θ)$ ，并不对分布本身进行建模，而是建模生成过程
  - 玻尔兹曼机(Boltzmann machine)/受限玻尔兹曼机(Restricted Boltzmann Machines，RBM)
  - 深度信念网络(DeepBelief Network，DBN）
  - 变分自编码器(Variational Auto-Encoders，VAE)
  - 生成随机网络(Generative Stochastic Network，GSN)
  - 生成对抗网络(Generative Adversarial Network，GAN)
非概率方式
- 主成分分析(Principal Component Analysis，PCA)/核主成分分析(Kernel Principal Component Analysis，KPCA)
- 线性判别分析(Linear Discriminant Analysis，LDA)
- 多维尺度变换(Multi-dimensional Scaling，MDS)
- 局部线性嵌入(Locally Linear Embedding，LLE)
- 自编码器(Auto-Encoder)/降噪自编码器(Denoising Auto-Encoder，DAE)
- K-均值(K-means)
- 层次聚类(Hierarchical clustering)
- 谱聚类(Spectral clustering)
- 潜在语义分析((Latent Semantic Analysis，LSA)

正则化（约束）方法

$l_1$ 约束
$l_2$ 约束
$l_1+l_2$ 约束
$l_{1,2}$ 约束
迹范数约束

损失函数

回归
- $l_2$ 损失(平方差损失)
- $l_1$ 损失
- Huber损失
- Tukey损失
分类
- 0/1损失
- 指数损失
- Hinge损失
- Ramp损失
- 交叉熵损失函数

评价指标

回归
- 均方误差(Mean Squared Error，MSE)
- 均方根误差(Root Mean Square Error，RMSE)
- 平方绝对误差(Mean Absolute Error，MAE)
分类
- 混淆矩阵(Confusion Matrix)
  
  真正样本(True Positive,TP) : 样本真实类别是正向的,模型预测的类别也是正向的
  真负样本(True Negative,TN) : 样本真实类别是负向的,模型预测的类别也是负向的
  假正样本(False Positive,FP) : 样本真实类别是负向的,模型预测的类别是正向的
  假负样本(False Negative,FN) : 样本真实类别是正向的,模型预测的类别是负向的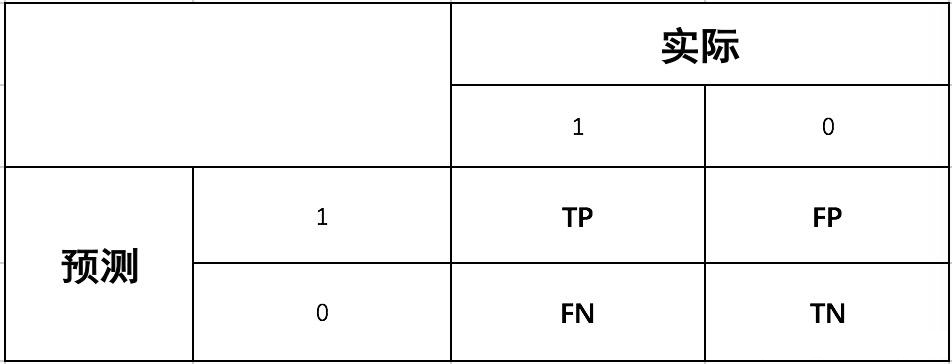
- 正确率(accuracy)
  
  $Accuracy=\frac{TP +TN}{TN+FN +FP +TP}$
- 精准率(Precision)
  
  $Precision=\frac{TP}{TP+FP}$
- 召回率(Recall)
  
  $Recall=\frac{TP}{TP+FN}$
- 特异度(Specificity)
  
  $Specificity=\frac{TN}{TN+FP}$
- F-值
  
  $F_{\beta}-Measure=\frac{(1+\beta^2)×Precision×Recall}{\beta^2×Precision+Recall}$
  
  当 $\beta=1$ 时候，即精准度和召回率一样重要的时候，公式如下：
  
  $F_1-Measure=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}=\frac{2×Precision×Recall}{Precision+Recall}$
- ROC曲线
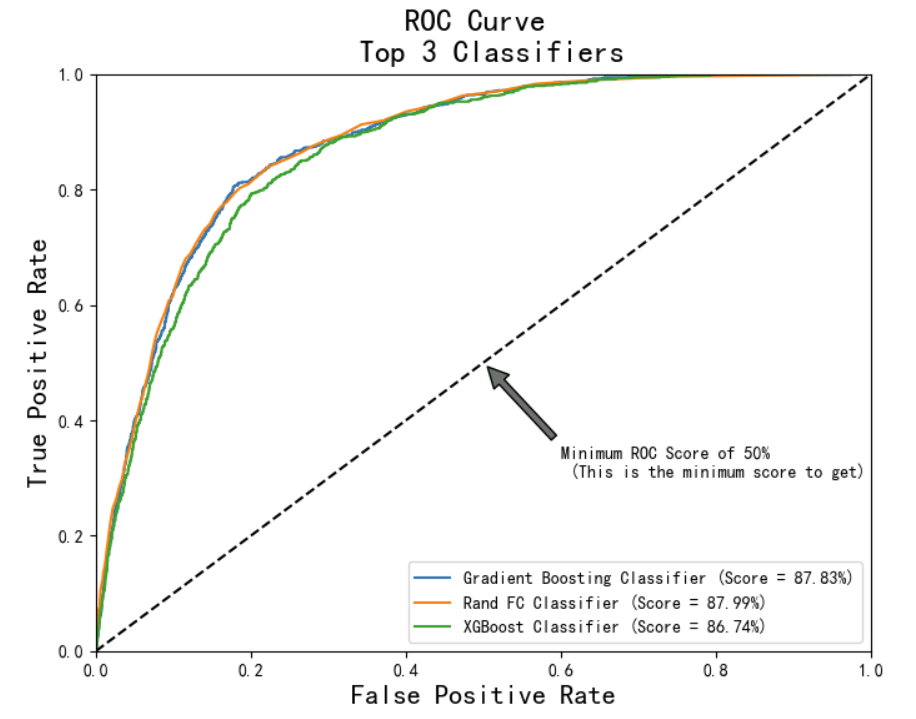
聚类
- 纯度(Purity)
- Rand指数
- 互信息(Mutual Information)